We are witnessing a revival of interest in the space of metric learning or representation learning, due to the popularity of embedding models in the NLP space. I thought of penning down some thoughts on the evolution of metric learning over the years, particularly from the point of view of computer vision.
Learning a powerful and generalizable representation has been of particular interest to researchers, as it has applications across a multitude of tasks like classification, person re-identification, face recognition, information retreival and recommender systems. It may be based on supervised, weakly supervised or unsupervised learning.
Classical machine learning approaches (nearest neighbours, SVM) relied on learning a linear distance metric based on a priori knowledge of data. With the advent of deep learning, we are able to learn non-linear feature mapping to learn scalable representations directly from images.
The core principle of deep metric learning is to learn a feature representation that brings similar entities closer and dissimilar entities further away, in the latent feature space.
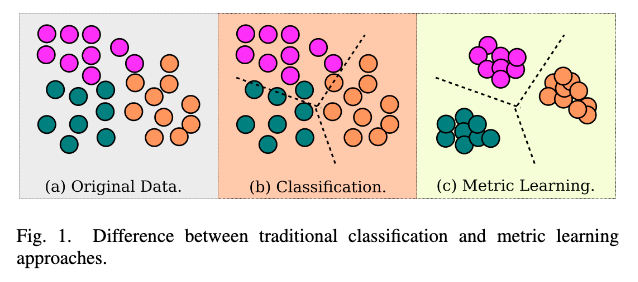
Advantages of Deep Metric Learning
A specific advantage of learning representations in this way, is that it helps the model handle unseen data. In the real world, a model may be exposed to data it was not trained on and it needs to perform reliably in such setting. This setting is often referred to as open-set problem.
Additionally, a compact representation in feature space will enable us to perform k-NN classification, clustering and information retreival with low dimension vectors.
Contrastive Methods
1. Constrastive Learning
Chopra et al. 2005 came up with the first contrastive learning approach towards deep metric learning. Their approach had two primary contributions:
- the metric was computed in the feature space rather than the input space
- the model was able to handle unseen data at test time
Contrastive loss takes a pair of inputs and minimizes the embedding distance when they are from the same class but maximizes the distance otherwise.
2. Triplet Loss
Emerging from research in face recognition, Triplet loss was first proposed in FaceNet (Schroff et al. 2015). The primary motivation of the researchers was to learn a Euclidean mapping for input data where distances directly correspond to measure of face similarity.
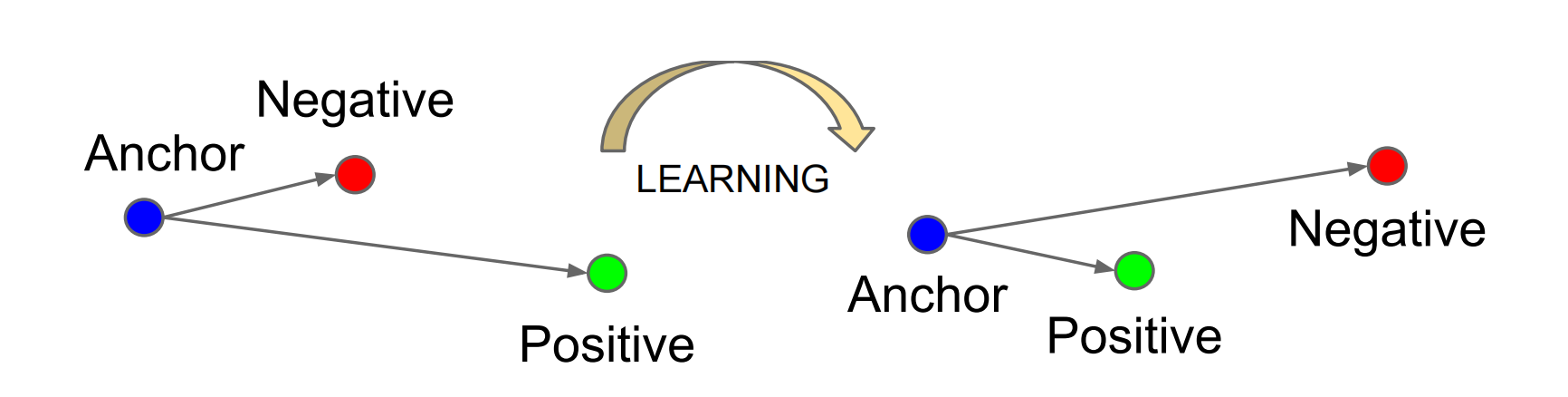
The formulation selects one anchor sample from a class, one positive sample that is of the same class and one negative sample that belongs to a different class. Triplet loss minimizes the distance between the anchor and positive and maximize the distance between the anchor and negative at the same time with the following equation: where the margin parameter is configured as the minimum offset between distances of similar vs dissimilar pairs.
Key Considerations
Hard negative mining - In every batch, the model needs to select hard samples for the negative to truly learn in every iteration.
Large batch size - These approaches rely on a relatively large batch size to compute loss.
Evaluation
Musgrave et al. published a technical report establising a benchmark and comparing the various metric learning approaches. The report claims that for majority of applications, triplet loss and contrastive margin loss perform superior to most mordern techniques.
They have an interesting implementation pytorch-metric-learning which comes plugged-in with various loss functions and mining methods.